Title: Asymptotically polynomial type solutions for 2-dimensional coupled non-linear ODEs with derivative terms

Authors: B.V.K. Bharadwaj; Pallav Kumar Baruah

Addresses: Department of Mathematics and Computer Science, Sri Sathya Sai Institute of Higher Learning, Prasanthinilayam – 515134, India ' Department of Mathematics and Computer Science, Sri Sathya Sai Institute of Higher Learning, Prasanthinilayam – 515134, India

Abstract: In this paper, we consider the following coupled system of non-linear ordinary differential equations.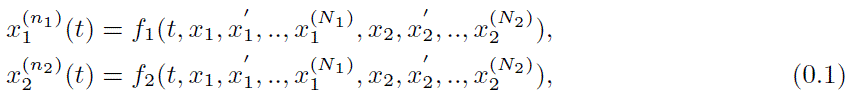

where ƒ1, ƒ2 are real-valued continuous functions on [t₀,∞) x R^N¹⁺^N² , t ≥ t₀ > 0, n_i > 1 and N_i are integers with 1 ≤ N_i ≤ min { n_i - 1, n₂ - 1 } for i = 1, 2. We give sufficient conditions on the non-linear functions ƒ1, ƒ2, such that the solutions pair 𝒳1; 𝒳2 asymptotically behave like a pair of real polynomials.

Keywords: non-linear coupled ordinary differential equations; fixed-point theorem; asymptotically polynomial like solutions; Schauder's theorem; generalised system; Magneto Hydodynamics; equiconvergent; equicontinous; compactness; uniformly bounded.

DOI: 10.1504/IJDSDE.2022.126528

International Journal of Dynamical Systems and Differential Equations, 2022 Vol.12 No.4, pp.339 - 360

Accepted: 26 Apr 2021
Published online: 28 Oct 2022 *

Full-text access for editors Full-text access for subscribers Purchase this article Comment on this article