Title: Existence and boundary behaviour of positive solutions for a coupled fractional system

Authors: Imen Ben Saad; Sameh Turki; Zagharide Zine El Abidine

Addresses: Department of Mathematics, Faculty of Science and Art, Khulais, University of Jeddah, Jeddah 22230, Saudi Arabia ' Department of Basic Sciences, Deanship of Preparatory Year and Supporting Studies, Imam Abdulrahman Bin Faisal University, P.O. Box 1982, Dammam 31441, Saudi Arabia ' Université de Tunis El Manar, Faculté des Sciences de Tunis, LR18ES09 Modélisation Mathématique, Analyse Harmonique et Théorie du Potentiel, 2092, Tunis, Tunisie

Abstract: We consider the following semilinear fractional system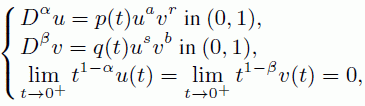

where α, β ∈ (0,1), a, b ∈ (-1, 1), r, s ∈ ℝ such that (1 -|a|)(1 - |b|) - |rs| > 0,D^α,D^β are the Riemann-Liouville fractional derivatives of orders α, β and the nonlinearities p, q are positive measurable functions on (0, 1). Applying the Schäuder fixed point theorem, we establish the existence and the boundary behaviour of positive solutions in the space of weighted continuous functions.

Keywords: system of fractional differential equations; boundary behaviour; Karamata class; Schäuder's fixed point theorem; Riemann-Liouville derivative; positive solutions.

DOI: 10.1504/IJDSDE.2022.125202

International Journal of Dynamical Systems and Differential Equations, 2022 Vol.12 No.3, pp.215 - 233

Accepted: 01 Sep 2020
Published online: 02 Sep 2022 *

Full-text access for editors Full-text access for subscribers Purchase this article Comment on this article